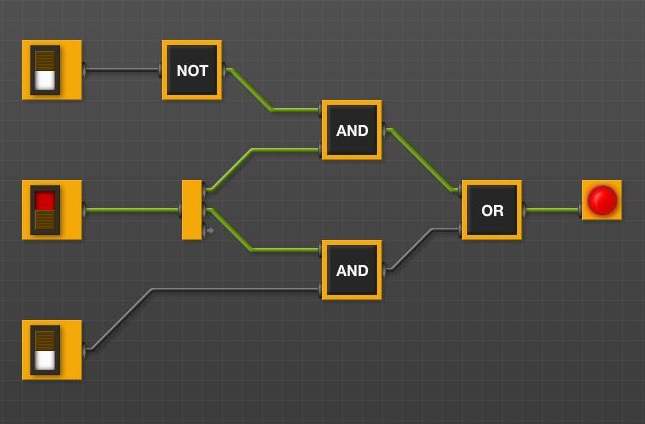
Portas Lógicas
Já vimos que uma função Booleana pode ser representada por uma equação ou detalhada pela sua tabela verdade. Mas uma função Booleana também pode ser representada de forma gráfica, onde cada operador está associado a um símbolo específico, permitindo o imediato reconhecimento visual. Tais símbolos são conhecidos por portas lógicas.
Na realidade, mais do que símbolos de operadores lógicos, as portas lógicas representam recursos físicos, isto é, circuitos eletrônicos, capazes de realizar as operações lógicas. Na eletrônica que trabalha com somente dois estados, a qual é denominada eletrônica digital, o nível lógico 0 normalmente está associado à ausência de tensão (0 volt) enquanto o nível lógico 1, à presença de tensão (a qual geralmente é 5 volts). As portas lógicas representam também circuitos eletrônicos que, de alguma maneira, realizam as funções Booleanas simbolizadas. Então, ao conjunto de portas lógicas e respectivas conexões que simbolizam uma equação Booleana, denominaremos circuito lógico.
Porta OU
O símbolo da porta OU pode ser visto na figura abaixo. Tal como na porta E, as entradas são colocadas à esquerda e a saída, à direita. Deve haver no mínimo duas entradas, mas há somente uma saída.
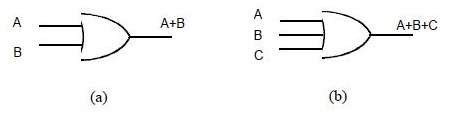
Símbolo da porta lógica OU com 2 entradas (a) e com 3 entradas (b).
Porta E
O símbolo da porta E é mostrado na figura abaixo. À esquerda estão dispostas as entradas (no mínimo duas, obviamente) e à direita, a saída (única). As linhas que conduzem as variáveis de entrada e saída podem ser interpretadas como fios que transportam os sinais elétricos associados às variáveis.
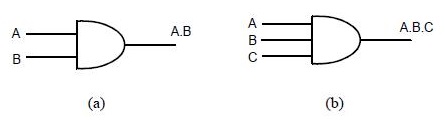
Símbolo da porta lógica E com 2 entradas (a) e com 3 entradas (b).
Inversor (ou Porta Inversora, ou Negador)
A porta que simboliza a operação complementação é conhecida como inversor (ou porta inversora, ou negador). Como a operação complementação só pode ser realizada sobre uma variável por vez (ou sobre o resultado de uma subexpressão), o inversor só possui uma entrada e, obviamente, uma saída. Caso se queira complementar uma expressão, é necessário obter-se primeiramente o seu resultado, para só então aplicar a complementação. O símbolo do inversor é mostrado na figura abaixo.
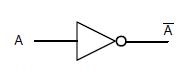
Símbolo do inversor (também conhecido como negador ou porta inversora).
Exemplo de Circuito Lógico
Dada uma equação Booleana qualquer, é possível desenhar-se o circuito lógico que a implementa. O circuito lógico é composto das portas lógicas relacionadas às operações que são realizadas sobre as variáveis de entrada. Os resultados das operações são conduzidos por fios, os quais, no desenho, são representados por linhas simples.
Os passos a serem seguidos para se realizar o desenho do circuito lógico a partir de uma equação são praticamente os mesmos usados na avaliação da expressão. Tomemos como exemplo a equação W = X + Y.Z'. Inicialmente, identificamos as variáveis independentes, que no caso são X, Y e Z. Para cada uma destas, traçamos uma linha (da esquerda para a direita), representando os fios que conduzem os valores. Feito isto, deve-se seguir desenhando as portas necessárias para representar cada uma das subexpressões, na mesma ordem tomada para a avaliação, ou seja:
1° parêntesis (dos mais internos para os mais externos);
2° operações E;
3° operações OU.
A figura abaixo mostra o circuito lógico para a equação:
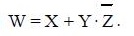
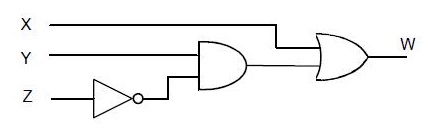
Leis Fundamentais e Propriedades da Álgebra Booleana
As leis da álgebra Booleana dizem respeito ao espaço Booleano (isto é., valores que uma variável pode assumir) e operações elementares deste espaço. Já as propriedades podem ser deduzidas a partir das definições das operações.
As operações elementares deste espaço são operação OU, operação E e complementação, cujas definições já foram dadas.
As propriedades da álgebra Booleana são as seguintes.


Propriedade Comutativa – OR
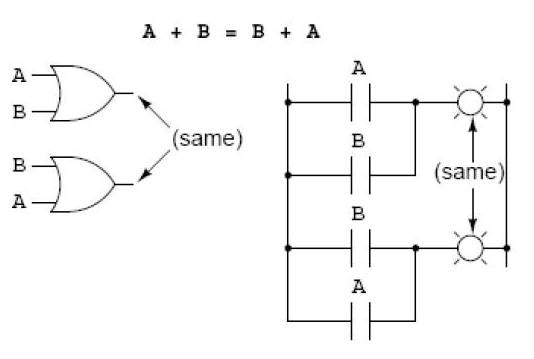
(same) significa igual ou mesmo.
Contatos Normalmente aberto (Normally-open) e Normalmente fechado (Normally-closed)

Na instrução Contato NA, o estado da saída digital é idêntico ao da entrada digital.
Na instrução Contato NF, o estado da saída digital é inverso ao da entrada digital.
Propriedade Comutativa – AND
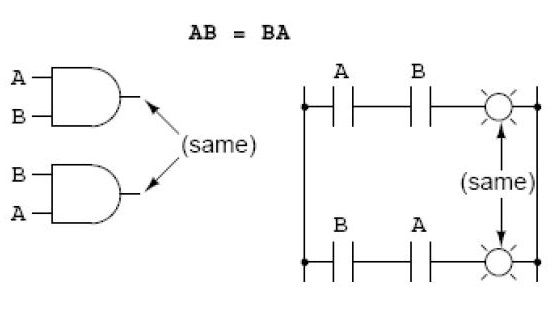
Propriedade Associativa – OR
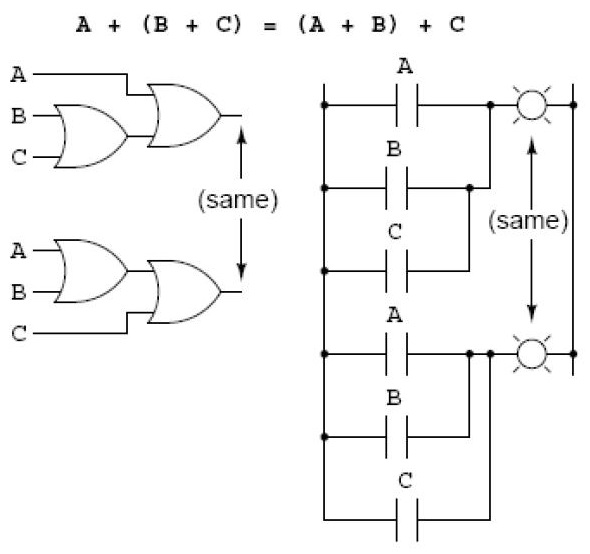
Propriedade Associativa – AND
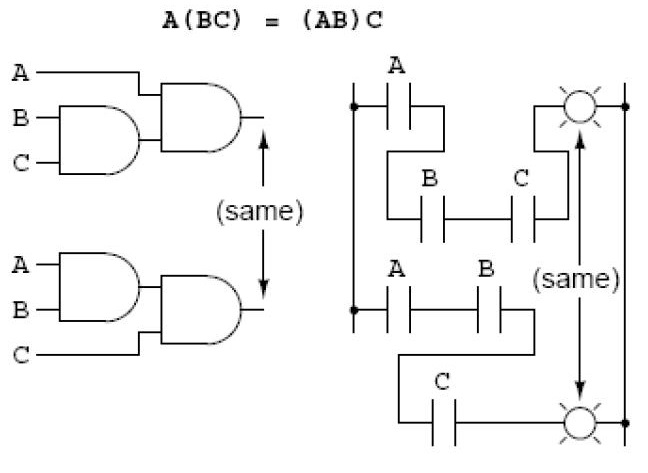
Propriedade Distributiva
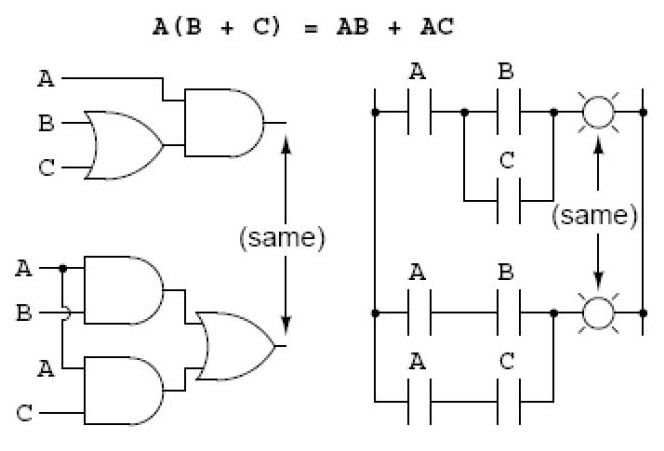
Observe que a expressão A . (B + C) contém duas portas lógicas (uma porta OR e uma porta AND) e a expressão AB + AC contém três portas lógicas (duas portas OR e uma porta AND). Os resultados das expressões são os mesmos, portanto, o circuito de A . (B + C) representa uma economia para o projeto de uma porta OR em relação ao circuito de AB + AC.
Outras Operações Lógicas
Até agora, tem-se visto apenas duas funções booleanas de duas variáveis, OU e E.
Mas, existem 22n funções Booleanas com n variáveis binárias. Assim, existem 16 funções Booleanas de duas variáveis e as funções E e OU são apenas duas dessas 16 funções. A tabela a seguir lista todas as 16 funções Booleanas de duas variáveis, x e y.
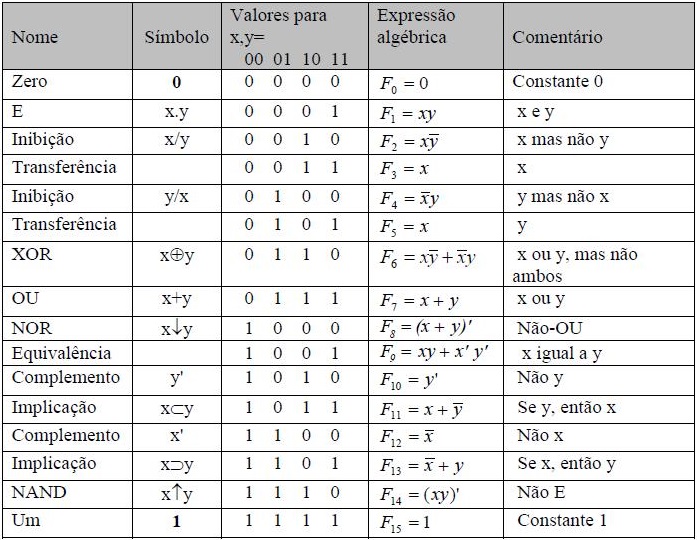
Cada linha na tabela acima representa uma função de duas variáveis e os nomes destas funções são dados na primeira coluna. As tabelas verdades de cada uma das funções são dadas na terceira coluna. Note que cada função foi designada por Fi onde i é o decimal equivalente ao número binário que é obtido interpretando-se os valores das funções dados na terceira coluna como números binários.
Cada uma destas funções pode ser dada em termos de operações E, OU e complemento. Como pode ser visto na tabela, existem duas funções constantes, 0 e 1, que retornam sempre 0 ou 1, respectivamente, independente de que valores se tem na entrada.
Existem quatro funções de uma variável, que representam o complemento e a transferência. E existem 10 funções que definem oito operações binárias: E, inibição, XOR, OU, NOR, equivalência, implicação e NAND. Sendo que inibição e implicação nunca são usados no projeto de circuitos, principalmente, por poderem ser facilmente implementados usando-se operações E, OU e complemento. A função NOR é o complemento da operação OU e a função NAND é o complemento da operação E. Pode-se notar também que XOR e equivalência são o complemento uma da outra e, por esta razão, a equivalência é normalmente chamada XNOR.
Para implementar as funções mostradas na tabela acima, são usadas geralmente oito tipos de portas lógicas: portas E, OU, complemento ou inversora, portas de transferência ou driver, portas NAND, XOR e XNOR.
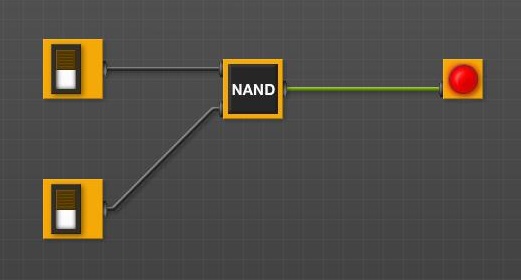
Porta NAND
Acessar LogicLab
• Acessar a página http://www.neuroproductions.be/logic-lab/index.php
• Configurar circuito com porta NAND.
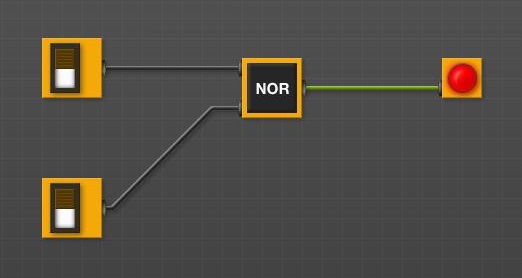
Porta NOR
Acessar LogicLab
• Acessar a página http://www.neuroproductions.be/logic-lab/index.php
• Configurar circuito com porta NOR.
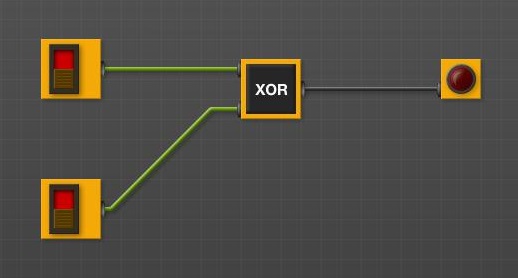
Porta XOR
Acessar LogicLab
• Acessar a página http://www.neuroproductions.be/logic-lab/index.php
• Configurar circuito com porta XOR.
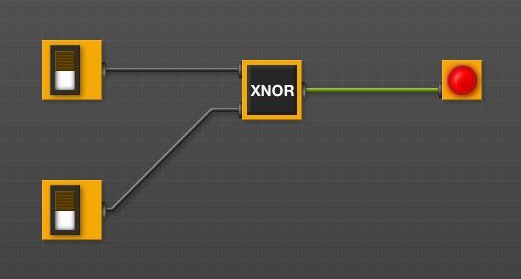
Porta XNOR
Acessar LogicLab
• Acessar a página http://www.neuroproductions.be/logic-lab/index.php
• Configurar circuito com porta XNOR.
A figura abaixo mostra portas lógicas com múltiplas entradas.
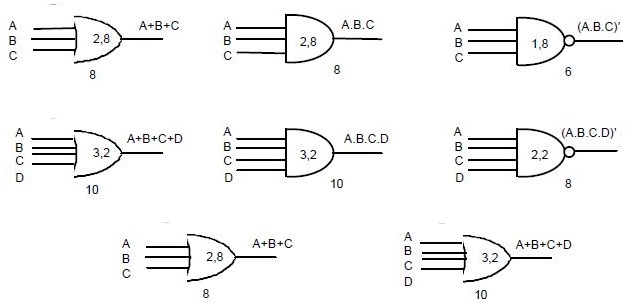
Circuitos Lógicos e Expressões Booleanas
Obtenha as expressões de X:
a) Um circuito lógico e suas expressões boolenas
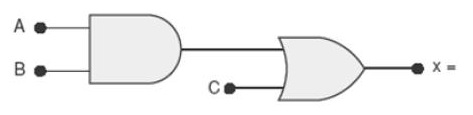
Resposta: X = A.B.C
b) Circuito lógico com uma expressão que requer parênteses
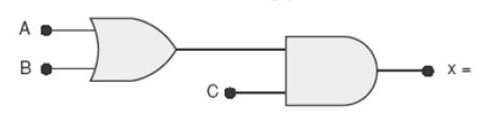
Resposta: X = (A+B).C
Circuitos com Inversores

c)
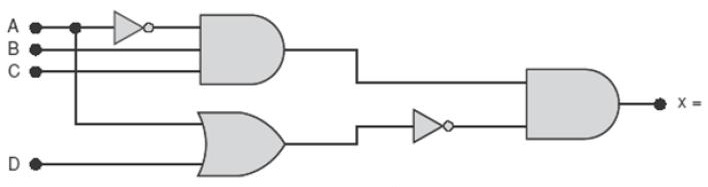
Resposta:
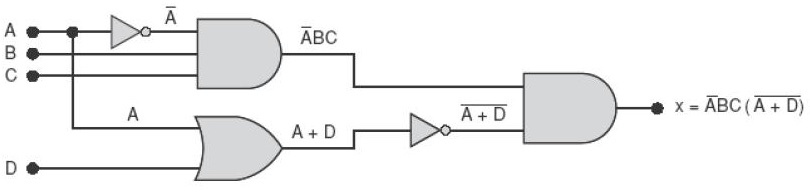
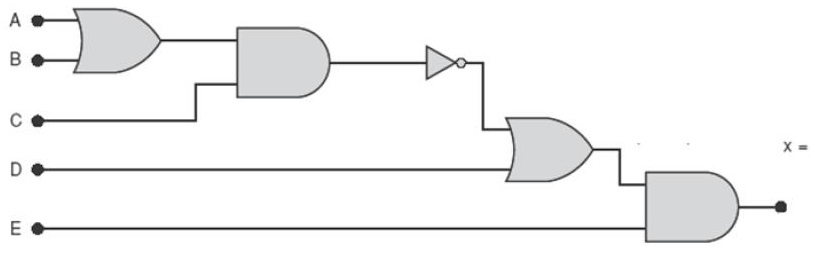
Resposta:
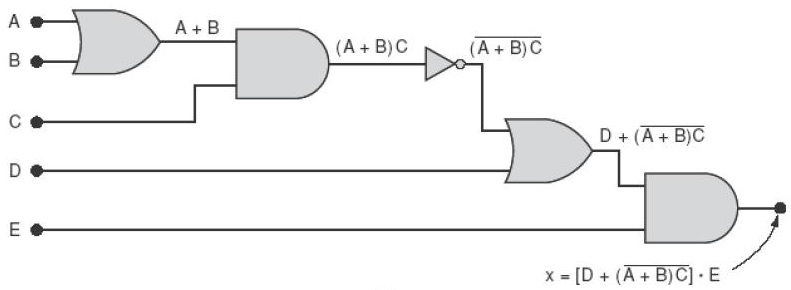
Obter a tabela verdade do circuito:
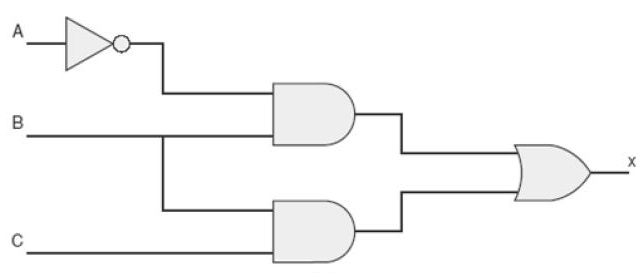
Desenha-se a tabela verdade com as colunas A, B, C, u = A', v = A'B, w = BC e x = v + w.
Preenche-se as colunas A, B e C com as 8 combinações diferentes (23 combinações). Preenche-se a coluna u = A' com o inverso de A.
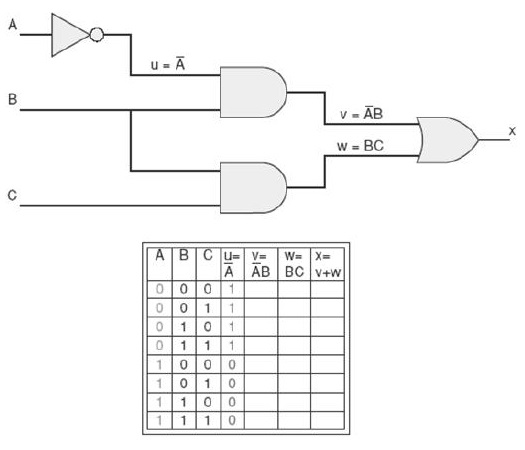
Preenchimento da coluna v = A'B:
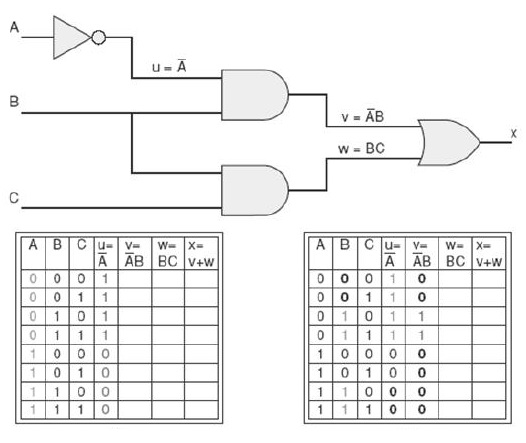
Preenchimento da coluna w = BC:
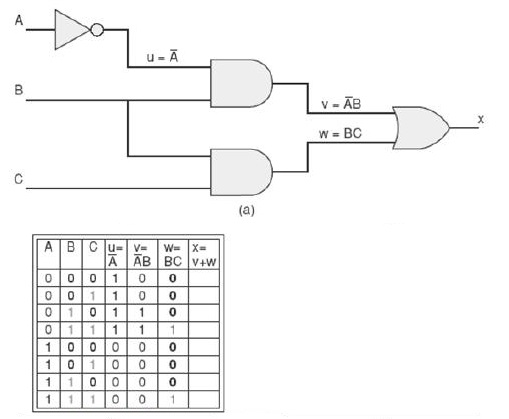
Preenchimento da coluna x = v + w:
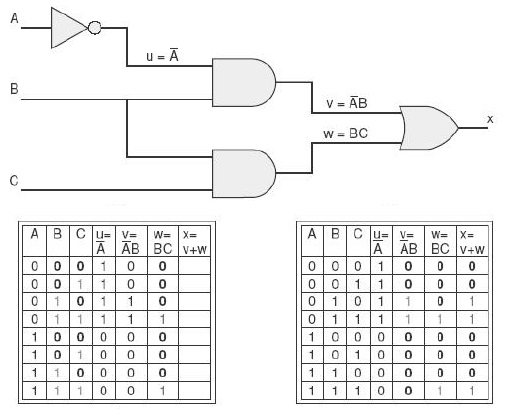
Acessar LogicLab e checar a validade da tabela verdade
• Acessar a página http://www.neuroproductions.be/logic-lab/index.php
• Configurar o circuito.